Nota: para mayor facilidad en la solución de estos ejercicios puedes copiar y pegar la información aquí contenida en un procesador de textos como Microsoft Word.
1. Realiza un breve resumen o un mapa conceptual en el cual expliques las propiedades del valor absoluto de los números reales y realiza un ejemplo de cada una.
2. ¿Qué significa resolver una ecuación y una inecuación con valor absoluto? Explica y realiza un ejemplo de cada una.
3. En la propiedad de la preservación de la división |a/b| = |a| / |b| (si b ≠ 0) ¿Por qué el valor que toma b, no puede ser cero?, Explica y propone un ejemplo.
4. ¿Cómo expondría o explicaría usted qué es un intervalo abierto y qué es un intervalo cerrado?
5. Observa el siguiente ejemplo:
- |x| < 2 -2 < x < 2 Es decir, x se encuentra en el intervalo entre -2 y 2, pero x no toma el valor de 2 ni de -2
Gráficamente tendríamos lo siguiente:
La parte rosada indica todos los valores que x puede tomar, es decir, x puede tomar cualquier valor en el intervalo entre -2 y 2, excepto esos dos valores.
- a. ¿Por qué x no puede valer 2, ni -2?, Argumenta.
Y en el siguiente ejemplo:
|x| ≤ 12 -12 ≤ x ≤ 12 Es decir, x se encuentra en el intervalo entre -12 y 12
Gráficamente tendríamos lo siguiente:
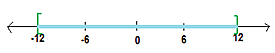
La parte azul indica todos los valores que x puede tomar, es decir, x puede tomar cualquier valor entre -12 y 12, incluyendo esos dos valores.
- b. ¿Por qué en este caso x, también puede valer 12 y -12?, Argumenta.
6. Resuelva las siguientes ecuaciones:
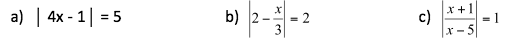
7. Resuelve cada una de las siguientes inecuaciones y escribe y representa gráficamente el conjunto solución.
|
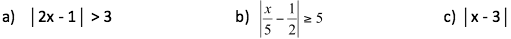
En esta página encuentras una sencilla explicación del concepto de valor absoluto y al finalizar puedes realizar la prueba denominada “comprueba si lo has aprendido” para que midas que tanto sabes sobre el tema. 
En estos dos enlace encontrarás información y ejemplos sobre Inecuaciones con valor absoluto