Propósito de la actividad
Esta actividad pretende que el estudiante demuestre comprensión de cada uno de los conceptos trabajados en la guía, los pueda representar de forma clara y coherente.
Descripción de la actividad
| |
|
|
| |
|
Descripción de la Actividad |
Resuelve el siguiente crucigrama.
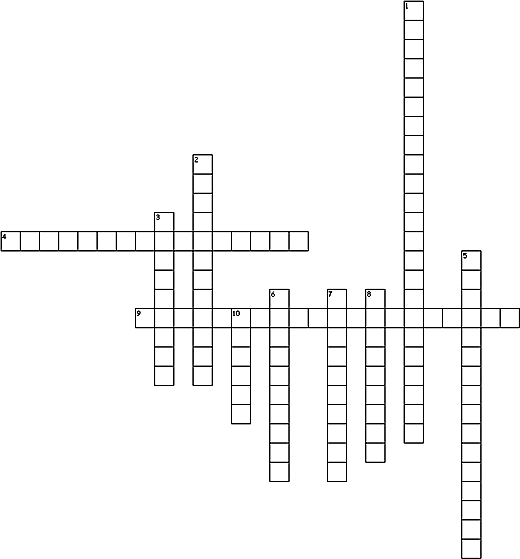
HORIZONTAL
4. Estas leyes permiten resolver problemas para triángulos que no son rectos.
9. Es una sucesión de números tales que cada uno de ellos (salvo el primero) es igual al anterior más un número fijo llamado diferencia que se representa por d.
VERTICAL
1. Es una sucesión de números tales que cada uno de ellos (salvo el primero) es igual al anterior multiplicado por un número constante llamado razón, que se representa por r.
2. Un triángulo que no es rectángulo se le llama.
3. Está considerado como el creador de la geometría analítica.
5. Es una curva plana cerrada formada por todos los puntos del plano que equidistan de un punto interior, llamado centro y cuya distancia común se llama radio.
6. Una de sus características es que tiene pendiente.
7. Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
8. Es el lugar geométrico de los puntos del plano cuya diferencia de distancias entre dos puntos fijos es constante y tiene asíntotas.
10. Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos es constante. Estos dos puntos fijos se llaman focos.
Completa la siguiente información sobre este interesante triángulo.
Una elegante silueta: el puente del Alamillo de Sevilla.
Fue construido entre 1989 y 1992 por el arquitecto Santiago Calatrava. El puente tiene un solo brazo que soporta todo su peso.
Es sin lugar a dudas una de las más destacadas construcciones de las llevadas a cabo en Sevilla con motivo de la Exposición Universal de 1992.
La estructura sustentadora, la plataforma de la calzada y los tirantes forman triángulos oblicuángulos semejantes.
Se les puede comentar a los alumnos que en esta unidad aprenderán a calcular la longitud de los diferentes tirantes conocidos los puntos
de anclaje en la calzada y la estructura sustentadora. La herramienta que se empleará es una generalización del teorema de Pitágoras.

- Estas figuras hacen referencia a las secciones cónicas. Identifícalas por el color y da una descripción de ellas.
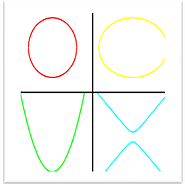 |
| color del grafico |
nombre de la secciones cónicas |
definición |
elementos que la constituyen |
| rojo |
|
|
|
| amarillo |
|
|
|
| verde |
|
|
|
| azul |
|
|
|
|
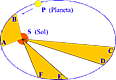
- Creemos que la tierra, junto con el sol y todo el sistema solar se mueve de manera conjunta alrededor de otras estrellas. Sin embargo este movimiento se creía era circular. Pero no. El movimiento que se describe es el de una elipse.
Teoría de Kepler
Como se mueve el sistema solar: |
¿No es el movimiento en forma circular de los planetas alrededor de la tierra? |
¿Es el movimiento en forma de elipse del sistema circular? |
Explica porque se mueve en forma de elipse y que es una elipse |

|
 |
|
|
- Di a que sección corresponde las siguientes ecuaciones.
| Ecuación |
¿Es una circunferencia, una parábola, una elipse o una hipérbola? |
Explica por que |
| y2-4x2=4 |
|
|
| x=2y2 |
|
|
| 9x2+4y2-18x+16y-11=0 |
|
|
| 3x2+3y2+12x-18y=-27 |
|
|
-
Observa con atención el gráfico y contesta las preguntas que se te formulan.
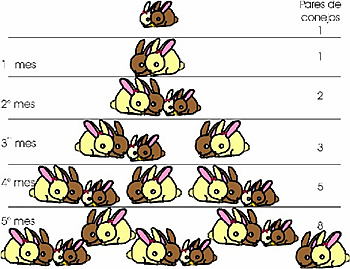
- ¿Cuántos pares de conejos situados en un área cercada se pueden reproducir en un año, a partir de un par de conejos, si cada par da lugar al nacimiento de uno por cada mes? Es decir; di cuantos conejos ahí a los 6 meses ,7 meses, 8 meses, 9 meses, 10 meses, 11 meses, 12 meses.
- Qué relación tiene esta actividad con Fibonacci y las progresiones.
|
|
|
|
| |
|
|